Принцип «камень, ножницы, бумага» в механических игрушках и его «родственные связи»

Пять лет назад я опубликовал две связанные статьи в журнале «Наука и жизнь»: «Правило транзитивности против нетранзитивности выбора» (№ 3, 2017) и «Нетранзитивность превосходства: продолжение темы» (№ 7, 2017). В них шла речь о нетранзитивных отношениях превосходства, метафорически называемых отношениями «камень, ножницы, бумага»: в одноимённой игре камень побеждает ножницы, те — бумагу, а бумага побеждает камень. В математике давно известны, активно изучаются и популяризуются нетранзитивные игральные кубики с такими числами на гранях, что кубик А чаще выигрывает у кубика В (показывает большее число на верхней грани), чем проигрывает ему; кубик В чаще выигрывает у С, а С чаще выигрывает у A*.
*Помимо статей, указанных выше, из недавних публикаций о таких кубиках можно упомянуть научно-популярную книгу: Шейнерман Э. Путеводитель для влюблённых в математику. Глава 19. Нетранзитивные игральные кости. — М.: Альпина нон-фикшн, 2018.
Вопрос — а можно ли изобрести механизмы, механические игрушки, взаимодействующие по принципу «камень, ножницы, бумага»? Эта тема была затронута в моих статьях в «Науке и жизни», здесь же я напишу о возможных ответах подробнее.
Нетранзитивные «мартышки». Посмотрев на рисунок, можно убедиться, эти три мартышки кормят друг друга нетранзитивным образом (красная — синюю, синяя — зелёную, а та — красную).

Нетранзитивные «помечальщики». Мартышки при кормлении могут ненароком закапать друг друга едой из ложки. Сделаем эту функцию основной. Из деталей «LEGO DUPLO®» с просверленными отверстиями и вставленными в них фломастерами можно соорудить такие три конструкции, что первая конструкция будет помечать своим фломастером вторую, оставаясь непомеченной ею, вторая — помечать третью, а третья — первую.
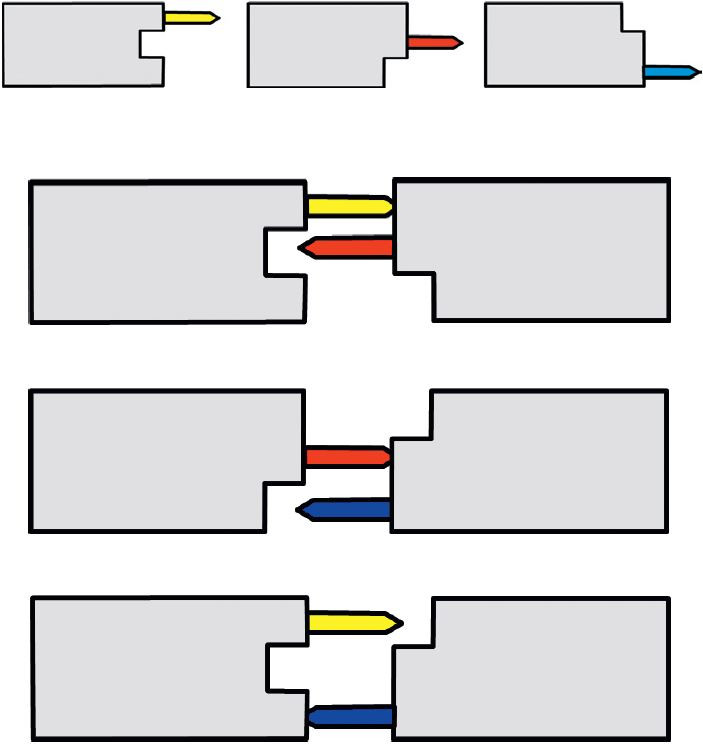
Нетранзитивные гребёнки. Кончик фломастера напоминает клин. Разовьём идею применения клиньев. Можно ли использовать клин как наклонную плоскость для таких нетранзитивных механизмов, при взаимодействии которых один поднимает другой? Возможный вариант показан на рисунке.
При фронтальном «наезде» гребёнка А своим профилем зубьев поднимает гребёнку В (она «сильнее»), В поднимает С, С поднимает А.
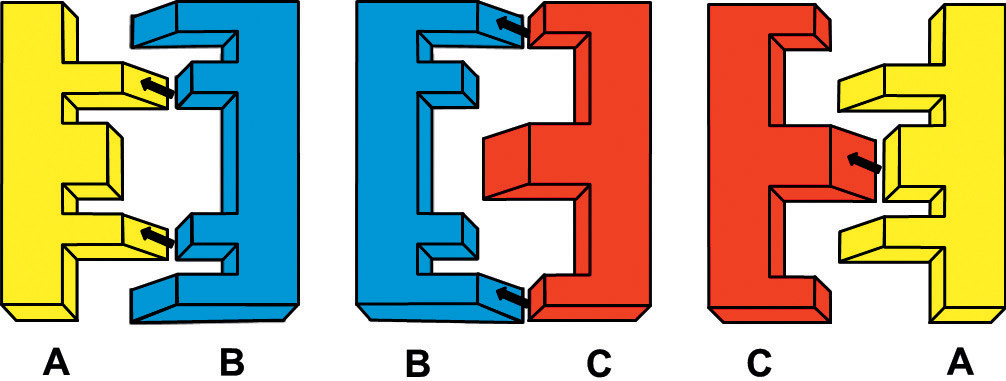

Нетранзитивные конструкции с рычагами. Перейдём к другому типу простых механизмов — рычагам. На рисунке показаны конструкции с креплением на валу длинных и коротких рычагов на разных уровнях. При равном усилии соревнующихся участников, приложенном к валам, конструкция А «пересиливает» В, В «пересиливает» С, С «пересиливает» А. Почему так происходит, читатель может подумать сам.
Можно устроить соревнование с использованием этих конструкций (назовём их двойными рычагами). Один участник выбирает какой-то понравившийся ему двойной рычаг. Второй участник, разбирающийся в механике, пусть и физически более слабый (например, в силу возраста), всегда может выбрать другой рычаг, который победит (пересилит) первый.
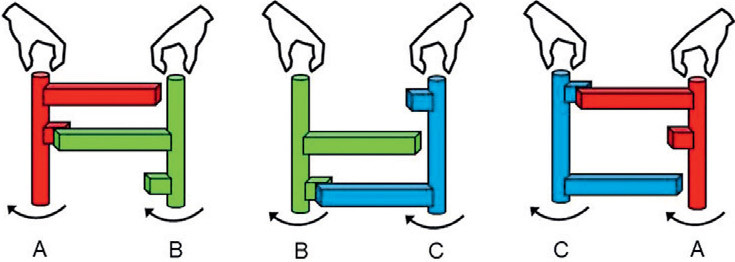
Нетранзитивные шестерни. Шестерни — ближайшие родственники рычагов в отношении способа передачи усилия. На рисунке показаны конструкции с бóльшими и меньшими шестернями, закреплёнными на валах на разных уровнях (так же, как в двойных рычагах). При попарных соединениях конструкция А вращается быстрее В в паре А-В, В вращается быстрее С в паре В-С, С вращается быстрее А в паре А-С. Если соединить все три конструкции вместе, вращаться они не смогут — их заклинит.
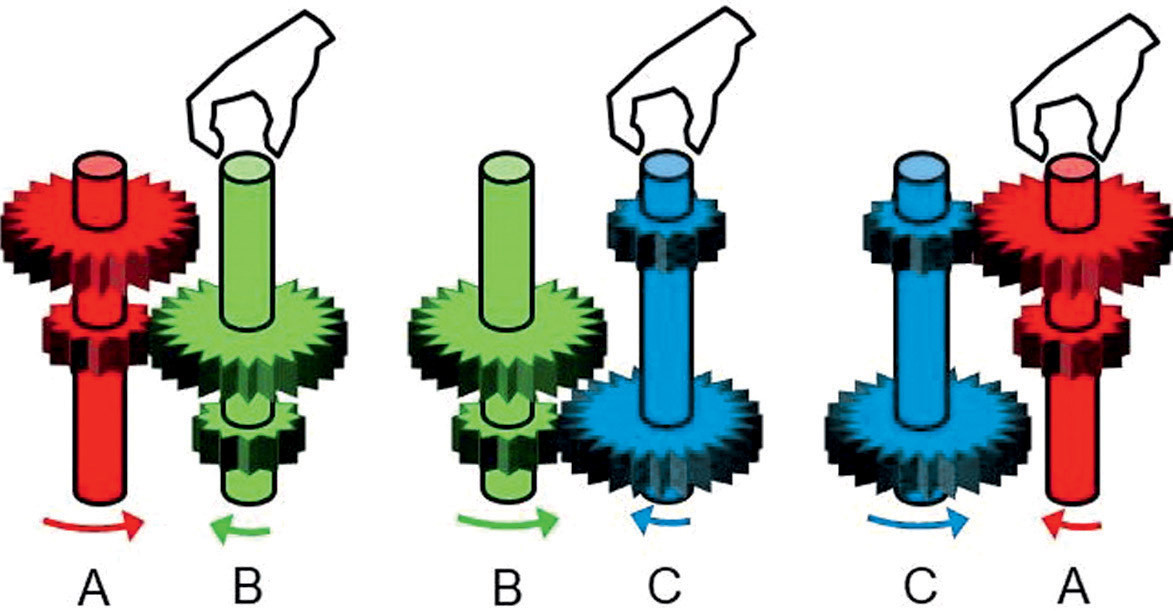
Действующую модель можно собрать из деталей детского конструктора «Gigo Junior Engineer 7333P Magic Gears» (с доработкой, поскольку оригинальные шестерни вращались на валах свободно — я закрепил их небольшими шурупами, а валы, наоборот, в плате не вращались — входили с усилием, и пришлось немного рассверлить отверстия).
