10 сложнейших математических задач, которые остаются нерешенными
На протяжении веков лучшие умы человечества решали одну математическую задачу за другой, однако есть несколько, не поддавшихся до сих пор никому. За нахождение алгоритма их решения некоторые фонды и компании готовы заплатить большие деньги.

Гипотеза Коллатца
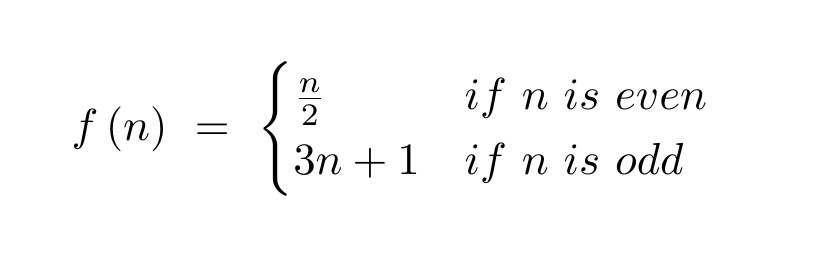
Другие названия: гипотеза 3n+1, сиракузская проблема, числа-градины. Если взять любое натуральное число n и совершить с ним следующие преобразования, рано или поздно всегда получится единица. Четное n нужно разделить надвое, а нечетное — умножить на 3 и прибавить единицу. Для числа 3 последовательность будет такой: 3x3+1=10, 10:2=5, 5x3+1=16, 16:2=8, 8:2=4, 4:2=2, 2:2=1. Очевидно, что если продолжить преобразование с единицы, то начнется цикл 1,4,2. Достаточно быстро количество шагов в вычислениях начинает превышать сто и на решение каждой новой последовательности требуется все больше ресурсов.
Небольшой прогресс в решении этой задачи почти вековой давности наметился буквально в прошлом месяце. Однако знаменитый американской математик Терренс Тао лишь ближе всех подошел к нему, но ответа все равно пока не нашел. Гипотеза Коллатца является фундаментом такой математической дисциплины, как “Динамические системы”, которая, в свою очередь, важна для множества других прикладных наук, например, химии и биологии. Сиракузская проблема выглядит, как простой безобидный вопрос, но именно это делает ее особенной. Почему ее так сложно решить?
Проблема Гольдбаха (бинарная)
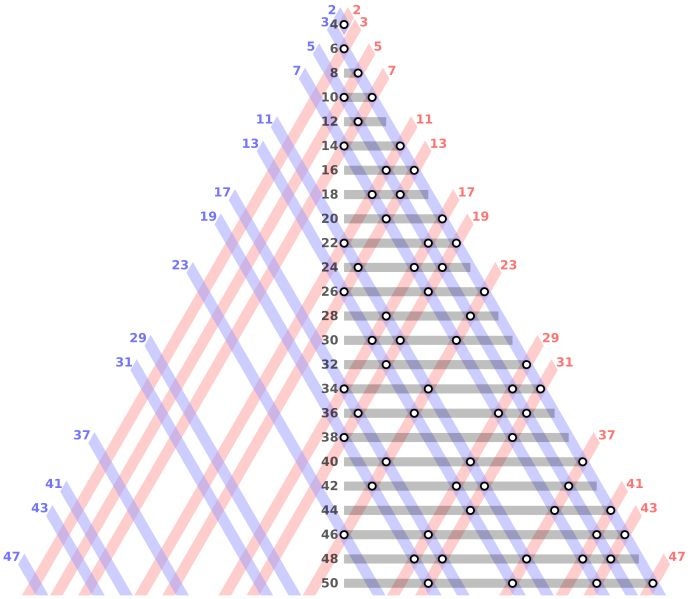
Еще одна задачка, формулировка которой выглядит проще пареной репы — любое четное число (больше 2) можно представить в виде суммы двух простых. И это краеугольный камень современной математики. Данное утверждение легко проверяется в уме для небольших значений: 18=13+5, 42=23+19. Причем рассматривая последнее, можно достаточно быстро понять всю глубину проблемы, ведь 42 представляется и как 37+5 и 11+31, а еще как 13+29 и 19+23. Для чисел больше тысячи количество пар слагаемых становится просто огромным. Это очень важно в криптографии, но даже самые мощные суперкомпьютеры не могут перебирать все значения до бесконечности, поэтому нужно какое-то четкое доказательство для всех натуральных чисел.
Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: "каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел". В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этого варианта. Однако предложенное Эйлером следствие этого утверждения, которое и назвали "бинарной проблемой Гольдбаха", до сих пор не поддается никому.
Гипотеза о числах-близнецах
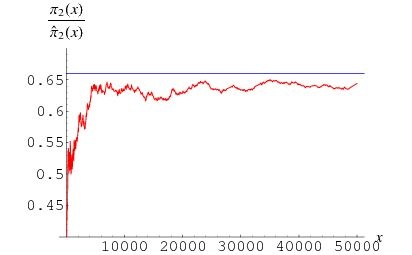
Близнецами называются такие простые числа, которые отличаются всего на 2. Например, 11 и 13, а также 5 и 3 или 599 и 601. Если бесконечность ряда простых чисел была доказана множество раз начиная с античности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, среди простых чисел нет четных, а начиная с 3 — делящихся на три. Соответственно, если вычесть из ряда все, подходящие под «правила деления», то количество возможных близнецов становится все меньше. Единственный модуль для формулы нахождения таких чисел — 6, а формула выглядит следующим образом: 6n±1.
