Отчаянные головоломки. Гигантские кубики

Когда многие ещё не успели разобраться, как решать кубик Рубика 3×3×3, изобретатели уже начали усложнять головоломку — увеличивать в ней количество слоёв. Раньше других в этом преуспел грек Панайотис Вердас (Panagiotis Verdes), придумавший механизм для производства кубиков 6×6×6 и 7×7×7. Своё изобретение он запатентовал в 2004 году, а его массовое производство началось в 2008 году. Но изобретатели не унимались, и спустя девять лет, в 2017 году, китайская компания «Shantou Yuxin Science and Educational Toys Co. Ltd» наладила серийный выпуск кубика 17×17×17.
Правда, серийная конструкция отличается от кубика 17×17×17 голландца Оскара Ван Девентера (Oskar van Deventer), представленного им в 2010 году на Нью-Йоркском симпозиуме любителей головоломок (New York Puzzle Party Symposium). Для изготовления кубика изобретателю пришлось распечатать на 3D-принтере 1568 деталей, не считая внутренних элементов конструкции.
Мировые рекорды по скорости сборки подобных гигантов не фиксируются. В российской части всемирной паутины можно найти ролик, автор которого утверждает, что собрал головоломку 17×17×17 менее чем за пять часов. Официальными признают рекорды, показанные на соревнованиях Всемирной ассоциации кубика (World Cube Association), где состязаются в скорости сборки кубиков 2×2×2, 3×3×3 и больших головоломок с четырьмя, пятью, шестью и семью слоями.
Рекорд скорости сборки кубиков размерностью больше 3х3х3 на момент написания статьи принадлежал американцу Максу Парку (Max Park). Любопытно, что Макс Парк — аутист и специально занялся скоростной сборкой кубика для развития мелкой моторики и решения проблем общения с окружающими. Таблица его результатов на разных соревнованиях приведена на в табл. 1.

Количество возможных состояний больших кубиков растёт по мере увеличения количества слоёв. Ниже приведены формулы расчёта количества комбинаций и итоговый результат (см. табл. 2). Число с восклицательным знаком означает факториал — произведение всех натуральных чисел, не превосходящих этого числа (например, 8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8).
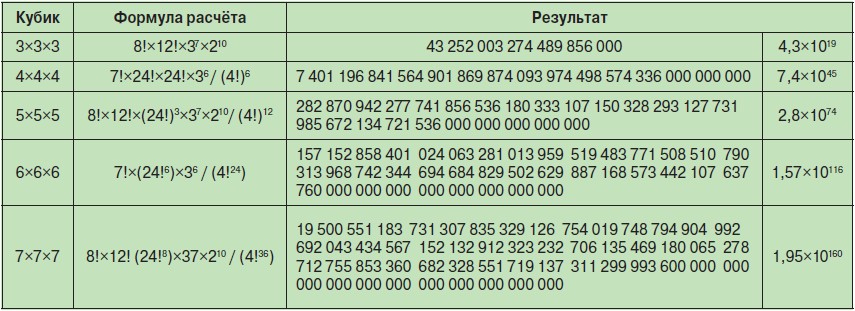
Напомним, что количество элементарных частиц во Вселенной, по оценке физика Тони Падилла (Tony Padilla), «всего-навсего» 3,28 x 1080.
Несмотря на обилие возможных состояний гигантского кубика его, в отличие от элементарных частиц, можно привести в порядок, то есть собрать. Решение этой задачи несколько сложнее; чаще всего используют алгоритм, который в итоге сводится к сборке кубика Рубика 3×3×3. Такой способ можно применять для решения головоломок как с чётным, так и с нечётным количеством слоёв.

Кубики, расположенные в вершинах гигантской головоломки, будем называть угловыми. Кубики на рёбрах — рёберными. Все остальные назовём центральными. Обычно план сборки гигантских кубиков следующий: сначала расставляют по местам центральные кубики. Затем собирают группы рёберных кубиков. Не обязательно, чтобы цвета рёбер при этом совпадали с цветами собранных центральных частей головоломки.
