Математики нашли многоугольник для апериодического паркета
Для доказательства апериодичности мозаики ученые показали иерархичность ее структуры
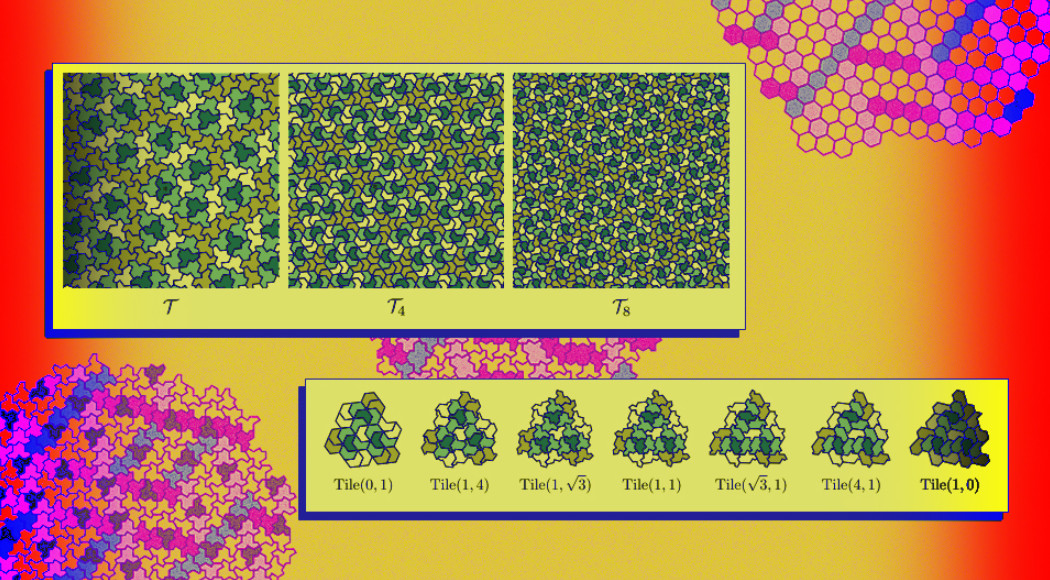
Математики нашли невыпуклый многоугольник, которым можно замостить плоскость только апериодически. Чтобы доказать принципиальную апериодичность паркета из таких элементов, ученые предложили свой собственный метод, в котором обосновывают геометрическую несоизмеримость иерархической структуры образующейся мозаики. По словам ученых, на основе найденного 13-угольника можно построить целый класс многоугольников с подобными свойствами. Препринт с результатами исследования опубликован на arXiv.org.
Замостить плоскость многоугольниками можно несколькими способами. Во-первых, можно создать периодический паркет, в котором элементы складываются в мозаику с трансляционной симметрией. То есть если сдвинуть ее в нужном направлении на нужное расстояние, то она наложится на себя. С помощью комбинаторных рассуждений можно доказать, что у выпуклых многоугольников в периодическом паркете может быть только три, четыре, пять или шесть сторон. При этом замостить плоскость можно любым трех- и четырехугольником, все подходящие пятиугольники делятся на 15 классов, а шестиугольники — на три. Подробнее паркетах из выпуклых многоугоульников — в нашем материале «Пять углов».
