Откуда вырос арифметический корень?

Студента, перекопавшего весь парк, спрашивают:
— Что ты делаешь?
— Да вот задание дали: найти квадратный корень. Третий день копаю, а только все круглые попадаются…
Анекдот.
Меня всегда интересовало, почему столь разные математические операции как извлечение корня и нахождение корня уравнений используют один и тот же термин — «корень» и какое отношение он имеет к известной части растений? Оказалось — самое прямое. Попробуем разобраться в запутанной истории появления на свет этих терминов и современного знака корня — радикала
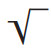
Решение задач, связанных с извлечением квадратного корня, археологи обнаружили ещё на вавилонских глиняных табличках, написанных около 4000 лет назад. Уже тогда древние математики находили стороны прямоугольного треугольника с помощью аналога будущей теоремы Пифагора, сторону квадрата — по известной площади и даже решали квадратные уравнения. Правда, каких-либо обозначений для квадратного корня на табличках найдено не было. Впрочем, до нашего времени их дожило слишком мало. А вот на двух египетских папирусах примерно того же времени, найденных в древнеегипетском городе Кахуне (Лахуне) в конце XIX века, имеется иероглиф

, который можно считать первым символом квадратного корня. Он удивительно схож с современным знаком! Если бы эти папирусы не были найдены столь недавно, можно было бы подумать, что наш знак корня позаимствован у древних египтян.
Наследниками этих древних цивилизаций были греки. Особых достижений они добились в области геометрии, к которой была сильно привязана математика. Если вам непонятно, как арифметика и даже алгебра могут быть описаны методами геометрии, надо просто представить, что возведение числа х в квадрат эквивалентно построению квадрата со стороной х, а затем измерению его площади. Отсюда, кстати, и произошёл термин «возвести в квадрат», а затем «квадратное уравнение» и подобные. Извлечение квадратного корня, наоборот, представляет собой задачу построения квадрата площадью х, а затем измерение его стороны. Так что у древних греков не было понятия корня, вместо него они использовали слова «сторона» — πλευρα и «основание» — βασιζ. Именно с них и начинается наша история.
Эту терминологию восприняли и продолжатели дела эллинов — древние римляне, только перевели на латынь. Латинское слово latus («сторона»), означающее корень, можно найти в дошедшем до нас труде римского землемера II века Марка Юния Нипса. От римлян пошла традиция сокращённо обозначать корень буквой l (L), используемая некоторыми европейскими математиками. Хотя это обозначение никогда не было популярным, оно продержалось достаточно долго, вплоть до XVII века, и применялось некоторыми известными учёными. Его можно встретить в трудах французского философа, математика и педагога Пьера де ла Раме (1515—1572), прославившегося тезисом «всё, сказанное Аристотелем, — ложно» и погибшего в Париже в ходе Варфоломеевской ночи. Наряду с другими обозначениями l использовал один из основоположников современной алгебры французский математик Франсуа Виет (1540—1603). Его теорему для корней квадратного уравнения изучают в школе. После изобретения логарифмов буква l была задействована для их обозначения. Любопытно, что англичанин Генри Бриггс (1561—1630), создатель первых таблиц десятичных логарифмов, тем не менее использовал l для обозначения корня.

Чтобы понять, как греческая «сторона» превратилась в «корень», нам придётся отправиться… в Индию! Казалось бы, при чём тут Индия, расположенная так далеко от Эллады? А «виноват» во всём Александр Македонский. В 327—325 годах до н. э. он завоевал значительную часть Северной Индии, которая впоследствии вошла в состав Государства Селевкидов, основанного после смерти Александра его полководцем Селевком. Индия имела древние традиции науки, но приход в эти края греческой культуры сильно подтолкнул её развитие.
Для нас важно появление в V веке научных сиддхант. Это понятие соответствует современным «доктрина» или «учение». Ранее оно относилось к богословию, а теперь так стали называть трактаты по астрономии и другим наукам. Первые сиддханты были явно эллинистического происхождения. Важнейшая из них написана индийским математиком и астрономом Брахмагуптой около 628 года. Она называлась «Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы») и состояла из 20 книг, в основном по астрономии, но две книги были посвящены математике. В них, в частности, учёный разработал методы нахождения квадратных корней и решений квадратных уравнений. Например, он довольно точно вычислил число π как √10 ≈ 3,162278. Любопытно, что в этот же период в Индии были изобретены цифры десятичной позиционной системы счисления, используемые нами и по сей день.
Большинство научных трактатов индийцев написаны на санскрите — языке религиозных книг брахманов. Этот язык играл роль латыни в Европе, он позволял понимать написанное людям, говорящим на разных языках. Греческие термины были переведены на санскрит как «пада» (сторона, основание) и «мула» (основание). Брахмагупта использовал слово «мула» и его сокращение «му», а оно имело также значение «корень». Это легко объяснить: корень можно считать основанием растения, на котором оно растёт. Вот и возникло слово «корень» в нашей истории, но его приключения на этом не закончились. Эллинистические государства в Азии к тому времени уже давно пали, их место заняли арабы. Корню пришлось возвращаться обратно в Европу окружным путём.
И здесь помог багдадский халиф Харун ар-Рашид, или Гарун аль-Рашид (766—809), известный по сказкам «Тысячи и одной ночи». Он основал в Багдаде библиотеку «Дом мудрости», которая впоследствии превратилась в крупнейшую своего рода исламскую академию наук, сделавшую Багдад на 500 лет интеллектуальным центром того времени. В ней работали выдающиеся учёные региона. Халифы собрали в библиотеке богатейшую коллекцию научных и философских трактатов на древнегреческом, индийском, китайском и других языках, многие из которых были переведены на арабский язык.
