Новый порядок
Куда (и почему) меняется значение слова «кристалл»

Часто так бывает, что одни и те же слова имеют разное значение — как для специалистов, так и обывателей. Например, «качественно» для ученых — не так уж и хорошо, по-настоящему качественное исследование должно приходить не к качественным (квалитативным) выводам, а количественным (квантитативным). Но это уже вполне устоявшаяся языковая конвенция. Есть термины, техническое значение которых прямо сейчас удаляется от привычного. Поговорим о кристаллах.
Большинство физиков все еще понимают под словом «кристалл» твердое тело, состоящее из периодически упакованных атомов. Но за последние десятилетия его стали применять к средам и явлениям, которые твердыми-то назвать нельзя. Рассказываем, что же такого некристаллического теперь в кристаллах — и почему.
Все современные значения слова «кристалл» продолжают отсылать к свойствам, которыми обладают традиционные кристаллы. В первую очередь — к трансляционной симметрии. Это значит, что если сместить бездефектную кристаллическую решетку традиционного кристалла на любое целое число периодов, то ее свойства не изменятся (равно как и свойства погруженных в нее электронов проводимости, электронных дырок, фононов и прочих квазичастиц).
Под бездефектностью решетки понимается в том числе и ее бесконечность. Такое не встречается в реальности. Однако практика показывает что такая модель работает хорошо, если строгий порядок сохраняется в пределах достаточно большого числа периодов. Это же касается и поликристаллических образцов, то есть образцов, состоящих из небольших монокристаллических доменов, ориентированных относительно друг друга под разными углами.
Это сказывается в первую очередь на электронах проводимости, которые путешествуют по всему кристаллу. Электроны рассеиваются на отдельных атомах, а не в непрерывной среде — это влияет и на то, как между собой связаны их энергия и импульс. То есть в кристалле меняются их дисперсионные соотношения: кинетическая энергия свободных электронов растет как квадрат импульса, а у электронов проводимости в кристалле эта функция становится периодической. Новая периодичность — уже в импульсном пространстве — позволяет ввести в нем обратную решетку (подробнее об обратных решетках мы рассказывали в материале «Тонко закручено»). Ее ячейки получили название зон Бриллюэна.
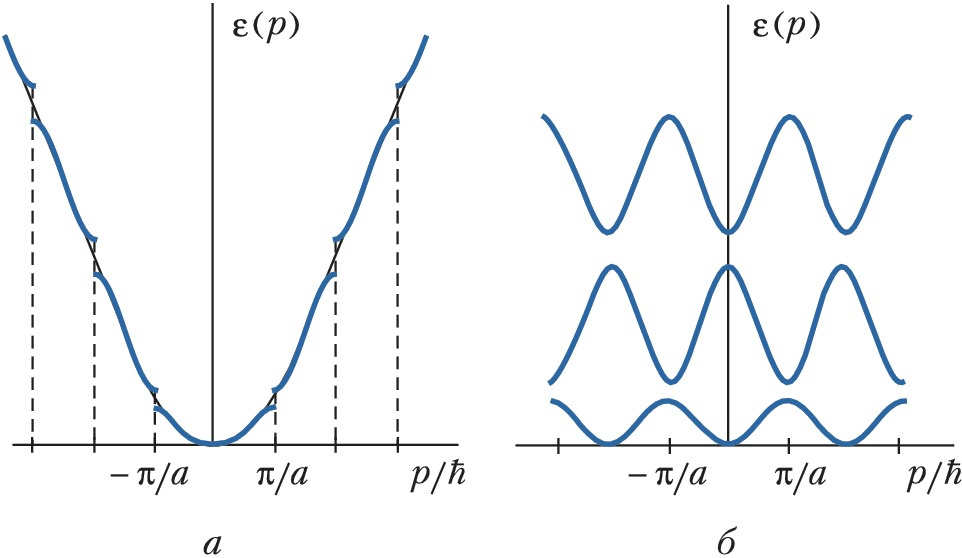
В бесконечной решетке физики следят за квазиимпульсом электронов — векторной величиной, которая описывает поведение электрона как квазичастицы внутри периодической решетки кристалла. Поскольку квазиимпульс периодический, то и определяют его в пределах одного периода в импульсном пространстве (одной зоны Бриллюэна).
Другая особенность кристаллов — в частичном нарушении закона сохранения импульса (точнее, квазиимпульса). Согласно теореме Нётер, сохранение импульса — это следствие однородности пространства, то есть неизменности законов физики относительно трансляций на любой вектор. Другими словами, все частицы продолжают вести себя так же, как и всегда, независимо от того, в какой точке пространства они находятся или куда двигаются. Но для электронов проводимости в кристаллах это не так. Из-за этого закон сохранения импульса справедлив только частично: импульс в кристаллических процессах сохраняется с точностью до целого числа периодов.
Впрочем, никакой фундаментальной беды здесь нет. Если помните, мы ведем речь о бесконечной решетке — а значит и масса у нее бесконечна. Если бы масса решетки была сопоставима с массой электрона, нам нужно было бы учитывать ее отдачу в процессах рассеяния, а закон сохранения импульса работал бы в полную силу.
