Впервые за десятилетия математики приблизились к разгадке таинственных "числ Рамсея"
Границы чисел Рамсея, которые описывают отношения между узлами в сети, наконец были сужены.
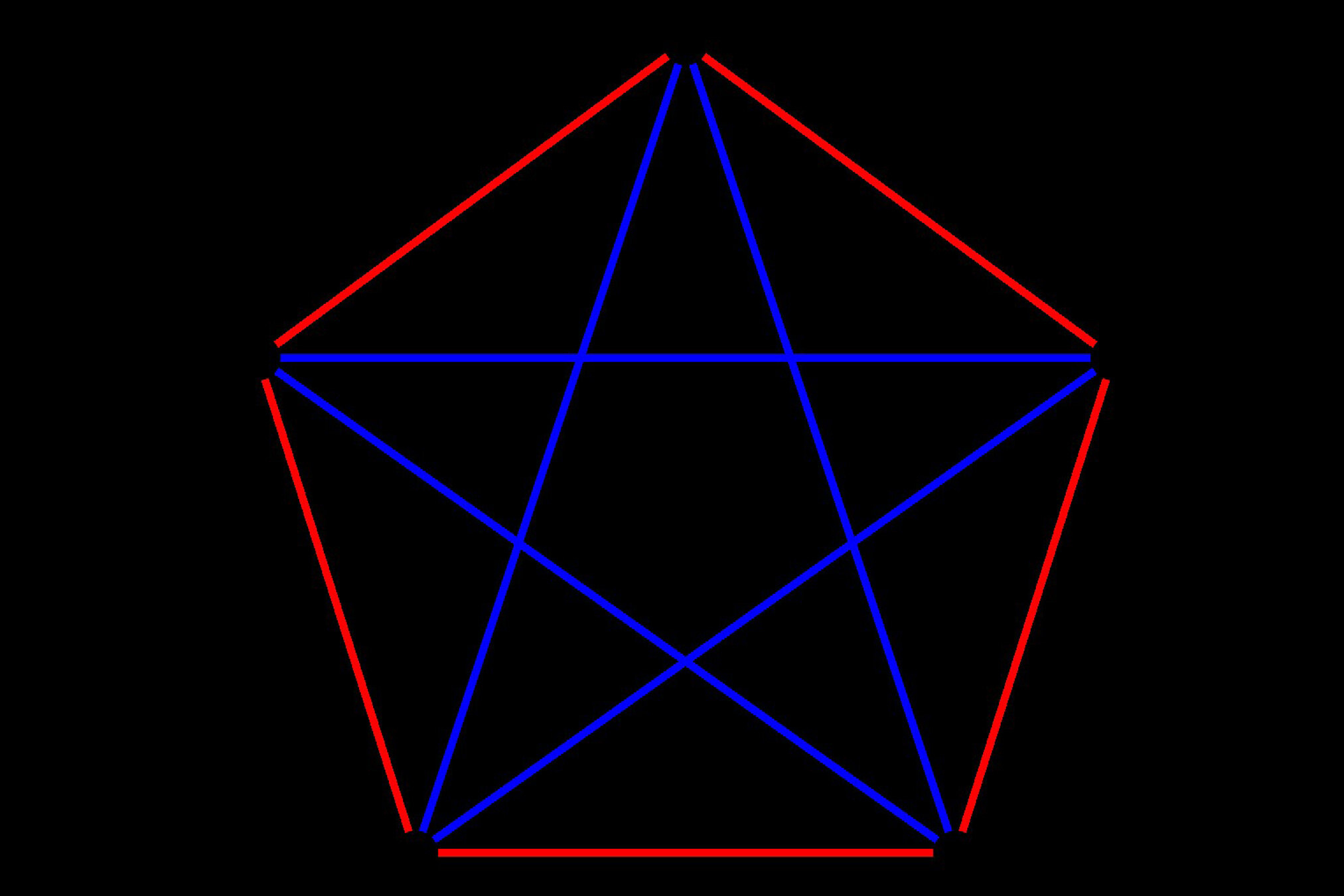
Проблема связана с числами Рамсея, обманчиво простой концепцией, но довольно скользкой с математической точки зрения. Число Рамсея — это минимальный размер группы, необходимый для того, чтобы определенное количество узлов в этой группе было соединено друг с другом. Самая распространенная метафора — вечеринка: сколько человек нужно пригласить на вечеринку, чтобы убедиться, что там будет либо группа из трех человек, которые будут знать друг друга, либо группа из трех человек, которые будут совершенно незнакомы?
Число Рамсея для 3 равно 6. И чтобы гарантировать, что на данной вечеринке будет группа из четырех друзей или четырех незнакомцев, вам нужно расширить список гостей до 18. Но каково число Рамсея для 5? Многие математики скажут вам, что оно лежит в пределе от 43 до 48. И по мере того, как числа становятся больше, проблема становится все более неразрешимой. Чем больше узлов в сети, тем больше возможных соединений и больше возможных структур для результирующего графа.
