О чём умолчали классики
Давайте перечитаем знакомые произведения русских писателей и рассмотрим их с точки зрения математики: выясним, какова скрытая мораль басни «Квартет», узнаем, далеко ли до края земли, и убедимся, что кот из лукоморья в самом деле учёный.

Неугомонный квартет
Вы конечно же помните басню Ивана Андреевича Крылова «Квартет» про четверых горе-музыкантов, где проказница Мартышка, Осёл, Козёл и косолапый Мишка затеяли пленить своим искусством свет. Достали инструменты, ноты, ударили в смычки, а толку нет. Попробовали сесть и так и этак, да ничего у них не вышло Вердикт эксперта Соловья был неумолим:
«Чтоб музыкантом быть, так надобно уменье
И уши ваших понежней...
А вы, друзья, как ни садитесь,
Всё в музыканты не годитесь».
Мораль сей басни математику ясна: переместительное свойство сложения по-прежнему незыблемо. Сумма зависит не от порядка слагаемых, а лишь от них самих. Так и в жизни: чем «весомее» слагаемые, тем лучше результат. А коли все они «нули», куда их ни поставь — получим тот же «нуль». Ещё, сдаётся мне, соображай герои басни в математике, им не пришлось бы обращаться к Соловью. Они бы не ругались, а просто подсчитали, сколько раз придётся пересаживаться, и, возможно, сразу отказались от своей затеи.
Решим эту комбинаторную задачу, но прежде вспомним, как развивались события до появления Соловья. «Музыканты» не только менялись местами, но и рассаживались по-разному. Мартышка предлагала сесть по кругу:
«Ты с басом, Мишенька, садись против альта,
Я, прима, сяду против вторы;
Тогда пойдёт уж музыка не та:
У нас запляшут лес и горы!»
Не помогло.
Затем Осёл «сыскал секрет» и заявил: «...мы, верно, уж поладим,
Коль рядом сядем».
Послушались Осла: уселись чинно в ряд,
А всё-таки
Квартет нейдёт на лад.
И пуще прежнего заспорили, кому и как сидеть...
Речь идёт о перестановках: нужно рассадить четверых «музыкантов» на четырёх местах сначала по кругу, а затем в ряд. Размещения одного типа будут отличаться друг от друга лишь порядком расположения участников квартета. В первом случае важно, кто с кем окажется рядом, а во втором — кто какое место займёт. Так сколько раз пришлось бы пересаживаться героям басни, чтобы перебрать все варианты?
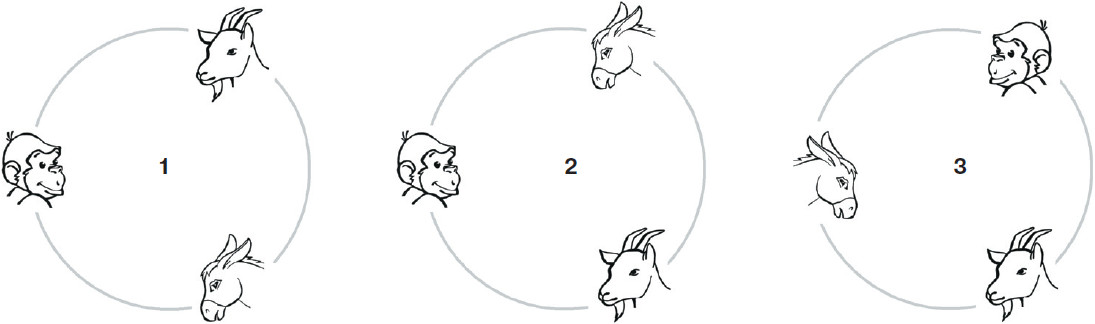
Троих персонажей можно рассадить по кругу двумя способами. Достаточно зафиксировать на месте кого-то одного, скажем Мартышку, и ещё двоих — Козла и Осла пересадить относительно неё*. Добавим к этим троим Медведя. В обоих случаях его можно разместить между любыми двумя персонажами, то есть тремя способами. Значит, для всей четвёрки насчитывается 6 вариантов размещения по кругу. Рассадить квартет в ряд получится уже 24 способами. На первом месте окажется по очереди каждый «музыкант», а остальные будут рассаживаться за ним на оставшиеся три места шестью разными способами. До появления Соловья из 30 возможных вариантов рассадки герои басни успели опробовать как минимум два.
* Если по команде «музыканты» переместятся в одном направлении и каждый займёт место соседа, положение всех троих относительно друг друга не изменится. Расположения, полученные одно из другого поворотом, считаются одинаковыми. Различными будут расположения, при которых соседи Мартышки меняются местами.
