«Вероятности и неприятности. Математика повседневной жизни»

Жизнь порой играет с человеком злую шутку: планы рушатся под давлением обстоятельств и случайностей, которые от нас как будто не зависят. В таких случаях говорят, что все происходит по «закону подлости». В книге «Вероятности и неприятности. Математика повседневной жизни» (издательство «Манн, Иванов и Фербер») кандидат физико-математических наук, популяризатор науки Сергей Самойленко ищет рациональное зерно и дает обоснование досадным закономерностям. Автор прибегает к теории вероятностей, а также смежным разделам: теории мер, марковским цепям, стохастическим процессам, теории очередей, динамическому хаосу и другим. N + 1 предлагает своим читателям ознакомиться с отрывком, в котором автор с помощью распределения Пуассона синтезирует жизнь, полную неприятностей, обнаруживает закономерности в наступлении плохих и хороших событий — и показывает, как это влияет на настроение человека.
Синтезируем злодейку-судьбу
Наступление событий, которые никак не связаны между собой и происходят во времени случайно, описывается с помощью хорошо известного пуассоновского потока. Он соответствует многим случайным явлениям — от землетрясений до прихода покупателей в магазин.
Предположим, выполнены такие естественные условия.
- Если есть два непересекающихся отрезка времени [t 1,t 2] и [t 3,t 4], то число событий в первом отрезке не зависит от числа событий во втором (отсутствие последействия).
- Количество событий, произошедших на каком-либо отрезке времени, зависит только от длины отрезка, но не его положения (стационарность).
- Вероятность, что два события происходят одновременно, пренебрежимо мала (ординарность). Тогда можно показать, что число событий, попадающих на отрезок длины t, подчиняется распределению Пуассона. То есть вероятность Pm того, что на этом отрезке произойдет m событий, определяется так:
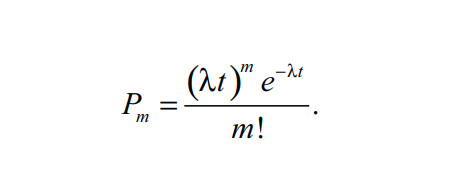
Число λ называется интенсивностью или плотностью потока и имеет смысл «среднего» числа наблюдений. Например, при измерении времени в днях значению параметра λ = 1/7 соответствует цепочка случайных событий, в среднем происходящих раз в неделю. Это вовсе не означает, что события будут происходить строго с частотой раз в неделю. Никакой определенной частоты у последовательности событий нет. Это среднее число событий: поскольку в году 52 недели, за год должно произойти около 52 событий (в среднем за много лет), но они будут разбросаны в году неравномерно. На рисунке 6.1 показаны 52 случайные равномерно распределенные даты в году, которые можно рассматривать как моменты появления пуассоновских событий.

Как видите, о какой-либо периодичности в этих событиях речь не идет: когда пожелают, тогда и случатся. Но и в этом беспорядке статистика может нам показать определенные закономерности. Например, распределение длительности периодов между событиями, показанными на предыдущем рисунке, будет вовсе не равномерным (рис. 6.2).
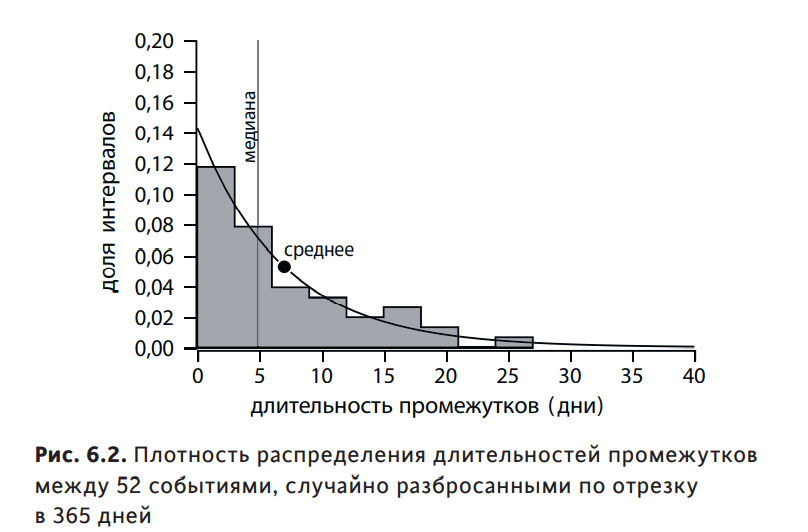
Промежутки времени между соседними пуассоновскими событиями имеют экспоненциальное распределение с плотностью λe–λt (на рисунке для нашего случая показана сплошной линией). У этого распределения максимум (мода) находится в нуле, а среднее значение равно 1/λ, в нашем случае 7 дней. Более того, стандартное отклонение σ тоже равно 7 дням, поскольку дисперсия экспоненциального распределения σ2 = 1/λ2. Как видите, эти характеристики вовсе не гарантируют того, что между событиями будет проходить одна неделя. В среднем — да, но чаще всего меньше; к тому же могут наблюдаться и достаточно долгие промежутки без событий. Наконец, медиана показывает, что половина всех промежутков будет иметь длительность не более 5 дней. Интенсивность и частота — совсем не одно и то же; это очень важное замечание, к которому мы еще вернемся в этой главе.
Для справедливости положим, что хорошие и плохие события происходят равновероятно, но яркие и значимые (как хорошие, так и плохие) — существенно реже мелких и незначительных. Пусть это будет «обычная» жизнь, в которой эмоциональная окраска событий подчиняется нормальному (гауссовскому) распределению. Вот как может выглядеть год синтетической судьбы в виде череды случайных абсолютно независимых жизненных перипетий (рис. 6.3).
