Дрессировка кошек Шрёдингера в промышленных масштабах

On s’engage, et puis on voit («Сначала надо ввязаться в бой, потом будет видно»).
Приписывается Наполеону
В фантастических романах главное это было радио. При нём ожидалось счастье человечества. Вот радио есть, а счастья нет.
И. Ильф. Записные книжки
Не отличись 2020 год многими другими странными событиями, он мог бы войти в историю как сорокалетний юбилей Второй квантовой революции. В 1980 году выдающийся советский математик Юрий Манин во введении к своей книге «Вычислимое и невычислимое» отметил, что квантовое вычислительное устройство — квантовый компьютер — будет обладать гораздо большим пространством состояний, чем классический с тем же числом элементов. Независимо от него в 1982 году ещё более выдающийся американский физик Ричард Фейнман в статье «Симулирование физики компьютерами» подошёл к вопросу с другой стороны: можно ли эффективно моделировать большую квантовую систему с помощью классических вычислительных устройств? И ответил: нет, её пространство состояний слишком велико, нужен именно квантовый компьютер.
Прежде чем рассказывать, какое отношение эти события имели ко Второй квантовой революции и что это за революция, нужно вспомнить, что такое «пространство состояний» и почему именно у квантовой системы оно так велико. Для простоты сравним набор обычных и квантовых битов.
Бит — это физическая система, которая может находиться в одном из двух возможных состояний («вверх-вниз», «право-лево», «вкл.-выкл.» и т. п.). Их удобно обозначать просто нулём и единицей. Набор из N битов может, таким образом, закодировать любое число от нуля до 2N –1 в двоичной системе счисления.
Квантовый бит, или кубит, отличается от обычного (классического) бита тем, что может находиться в любой суперпозиции состояний 0 и 1. Используя обозначения, введённые почти сто лет назад Полем Дираком, это можно записать так:
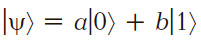
Здесь |ψ〉 — состояние кубита, а величины a и b, такие, что |a|2 + |b|2 = 1, говорят о том, чего в состоянии кубита «больше» — нуля или единицы. Это не значит, что если состояние кубита измерить, то получится что-то среднее между ними. Всегда получится либо ноль, либо единица — но если взять и измерить много кубитов в одном и том же состоянии |ψ〉, то доля тех, которые дадут ноль, будет |a|2, а тех, которые дадут единицу, — |b|2. Предсказать, что именно получится при каждом измерении, нельзя. Это не недостаток теории, а принципиальное свойство природы, очень хорошо подтверждённое и экспериментами, и практикой: природа принципиально случайна.
При слове «измерение» не нужно непременно представлять себе учёного с измерительным прибором. Этим словом для краткости обозначают любое взаимодействие кубита с окружающим миром, которое заставляет его в конце концов занять одно из состояний |0〉 или |1〉. В таком случае говорят, что измерение разрушает квантовую суперпозицию.
Однако вернёмся к кубиту до того, как его измерили. Чтобы описать его состояние |ψ〉, нужно не два числа, а целое двумерное пространство. Как для того, чтобы задать точку на плоскости, нужны координаты x и y, так и здесь нужны два числа, a и b. Эти числа не простые, а комплексные, но здесь это не принципиально. Важно то, что кубит «живёт» в двумерном пространстве. По сравнению с классическим битом, «живущим» всего в двух точках (0 и 1), квантовый бит — буквально властелин бесконечности.
Если теперь взять два кубита, то им потребуется уже четырёхмерное пространство. Действительно, два кубита могут находиться в любой суперпозиции четырёх состояний |00〉, |01〉, |10〉, |11〉 (здесь первая цифра говорит о состоянии кубита номер один, а вторая — кубита номер два), и для её описания нужно четыре числа, a, b, c ,d. Для трёх кубитов таких чисел потребуется уже восемь: каждый лишний кубит может быть в двух состояниях, поэтому число коэффициентов удваивается.
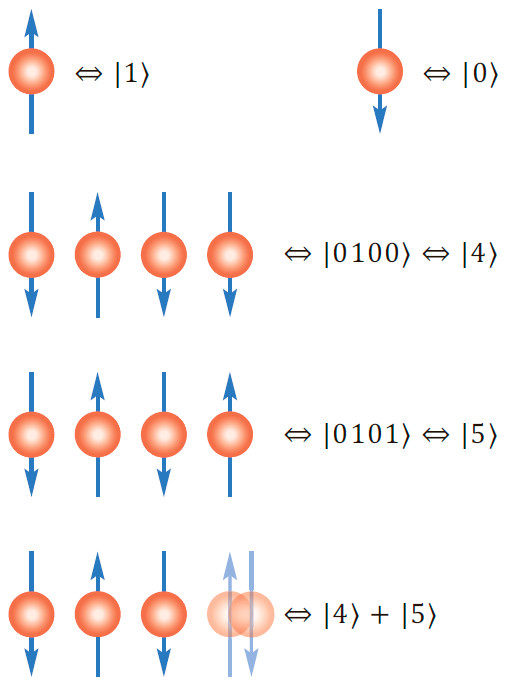
Система из N кубитов обитает в пространстве размерностью 2N. Это значит, что для задания состояния 50 кубитов нужно задать 1 125 899 906 842 624 координаты, а для 5000 кубитов — больше чем 101505 координат (для точной записи этого числа потребовалось бы полстраницы цифр). Число атомов в наблюдаемой Вселенной не превышает 1080 и уместилось бы меньше чем в две строки. Неудивительно, что эффективно промоделировать поведение даже такой небольшой квантовой системы не сможет никакой классический компьютер.
Теперь перейдём ко Второй квантовой революции. Сначала, естественно, надо упомянуть Первую, тем более что на её достижениях стоит значительная часть современной цивилизации. Первая революция произошла в середине прошлого века, когда результаты квантовой механики применили в технике. Изначально таким применением было, естественно, военное — как и в большинстве передовых технологий в истории человечества, от стали и взрывчатки до радаров и ракет. Атомное оружие и атомная энергетика стали прямым результатом использования квантовой теории в ядерной физике и большим стимулом к её дальнейшему совершенствованию. Затем последовали электроника и сверхпроводниковые устройства, основанные на квантовой теории конденсированного состояния (то есть всего, что не газ и не плазма), и лазеры — на квантовой теории света и его взаимодействия с веществом. Без Первой квантовой революции вы не читали бы эту статью с экрана компьютера или смартфона, не пользовались бы интернетом.
Сейчас вам захочется остановить меня и сказать: что-то у вас тут не сходится. Лазеры, компьютеры и атомные бомбы содержат не тысячи, а триллионы триллионов атомов. Как же можно было описать и предсказать их поведение, пользуясь даже не обычными компьютерами, а карандашом, бумагой и логарифмической линейкой? Это совершенно законный вопрос, ответ на который — всё сходится. Просто нам всем невероятно повезло.
Дело в том, что квантовые эффекты, лежащие в основе Первой революции, затрагивают за раз очень небольшое число квантовых объектов или, выражаясь точнее, небольшое число квантовых степеней свободы (то есть независимых переменных, нужных для описания данного явления). Скажем, в квантовой теории конденсированного состояния достаточно часто можно свести описание поведения огромного числа взаимодействующих между собой электронов и ионов к поведению почти не взаимодействующих между собой квазичастиц. (Именно в этом нам и повезло.) В металле это так называемые электроны проводимости и фононы, в полупроводнике — электроны проводимости, фононы и дырки. Их, конечно, очень много, но раз они не взаимодействуют между собой, их можно рассматривать по отдельности, и задачу иногда можно решить вообще без компьютера, с помощью карандаша и бумаги. В сверхпроводниках ситуация сложнее; там образуется макроскопическое квантовое состояние, занимающее весь объём сверхпроводника. Но хотя в нём участвует заметная доля всех электронов сверхпроводника, это состояние можно описать всего лишь одним комплексным числом (которое называется «параметр порядка»), зависящим от одной пространственной координаты, так что и там мы имеем дело с небольшим числом квантовых степеней свободы. Говоря более формально, в Первой квантовой были задействованы квантовые эффекты, не использующие квантовые корреляции высокого порядка.
Покажем разницу на примере системы (регистра) из трёх кубитов. В регистр из трёх классических битов можно записать любое двоичное число от нуля (000) до семи (111). Но каждый квантовый бит независимо от других может быть в суперпозиции состояний 0 и 1. Поэтому состояние всего регистра можно записать как
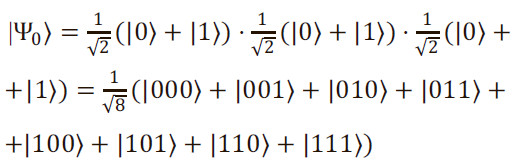
Таким образом, в квантовый регистр можно записать все числа от нуля до семи одновременно. Эта удивительная возможность вовсю используется в квантовых алгоритмах, но её одной было бы совершенно недостаточно. Дело именно в том, что в состоянии |ψ0〉 все кубиты независимы. Если один из них перестанет находиться в суперпозиции и «свалится» в состояние 0 или 1, другие этого не почувствуют: каждый по-прежнему останется в суперпозиции своих состояний 0 и 1. Говорят, что состояние |ψ0〉 факторизовано (то есть может быть записано как произведение состояний отдельных кубитов).
Совсем другое дело, если регистр находится в так называемом состоянии Гринберга—Хорна—Цайлингера
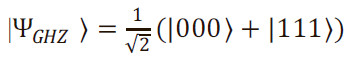
Если мы измерим состояние кубита номер один, то суперпозиция его состояний разрушится — он окажется в состоянии 0 или 1 с одинаковой вероятностью ½. Беда в том, что все оставшиеся кубиты окажутся в том же состоянии, что и первый кубит. Из-за измерения только одного кубита ни один кубит не останется в суперпозиции квантовых состояний. Другими словами, если суперпозиция состояний хоть одного кубита разрушена, то разрушено квантовое состояние сразу всего регистра.
Такие квантовые состояния, в которых измерение одного кубита влияет на остальные, называются запутанными (или спутанными). |ψGHZ〉 — пример квантового состояния, в котором запутаны три кубита. А для того чтобы квантовые алгоритмы сработали для сколько-нибудь практически интересных задач, потребуются запутанные состояния не трёх, а сотен и тысяч кубитов.
Что может разрушить суперпозицию состояний одного кубита? Да что угодно! Флуктуации электромагнитного поля, тепловые колебания кристаллической решётки материала кубита или его окружения, в общем, то, что называется «шум». Любое достаточно сильное взаимодействие с окружающим миром может привести к тому, что вместо суперпозиции кубит окажется либо в состоянии |0〉 (с вероятностью |a|
